B3 ascertains and publishes statistics for Overnight DI Rate (Extra-Group) securities, which are calculated based on fixed-rate Interbank Deposit issuances, agreed upon for one business day and registered and settled through the B3 system, as stipulated by the Central Bank of Brazil.
One-day (overnight) transactions are selected in the interbank market, exclusively considering transactions between institutions from different business groups (Extra-Group) and disregarding any others (Intra-Group). These statistics are, therefore, calculated from the fixed-rate Overnight DI (Extra-Group) population.
As of October 01, 2018, the DI Rate calculation methodology shall be based on compliance or non-compliance with the following two conditions:
- The number of transactions eligible for DI Rate calculation is 100 (one hundred) or more;
- The sum of transaction volumes eligible for DI Rate calculation is BRL 30 (thirty) billion or more.
If at least one of the two conditions defined in items I and II above does not occur on the day the DI Rate is calculated, the DI Rate will be equal to the Overnight SELIC Rate (Taxa Selic Over) published on the day*.
DI Rate = Overnight SELIC Rate*
- *If the Overnight SELIC Rate is not published by 09:00 p.m., B3 may use the Overnight SELIC Rate published on the previous business day for the purposes of calculating the DI Rate. In the event of non-publication of the Overnight SELIC Rate on the next business day after publication of the Target SELIC Rate (Taxa Selic Meta) by the Central Bank of Brazil’s Monetary Policy Committee (COPOM), B3 may use the Overnight SELIC Rate for the previous business day, adjusted as appropriate for any variation in the Target SELIC Rate set by the COPOM meeting. It is important to note that once the DI Rate has been announced, it will not be recalculated even if the Overnight SELIC Rate for the day is published later.
If on the day of the DI Rate calculation, the conditions of both items I and II above are met, the calculation methodology proposes that calculation be based on groups of rates and values, in accordance with the methodology in effect since October 07, 2013 and described below. In this treatment, there is no 5% (five per cent) exclusion at the extreme end (upper and lower) of the tails, but rather a dilution of the alpha percentage, which is defined at 10%, across the entire series of data. Therefore, the tail weights are reduced and distributed proportionately in the remaining weights, as defined in the item below.
DEFINITION OF THE OVERNIGHT RATE EXPRESSION IN EACH TRANSACTION
Rates are expressed annually, in accordance with the following formula:
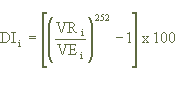
Where:
DIi - is the DI Rate of the i-th transaction, with calculation rounded off to two (2) decimal places.
VRi- is the Redemption Value of the i-th transaction, informed to two (2) decimal places.
VEi - is the Issue Value of the i-th transaction, informed to two (2) decimal places.
ABOUT THE OVERNIGHT DI RATE CALCULATION PROCESS:
1. Transactions are placed in an ascending order and then grouped together forming the binomial (rate; volume);
2. Each rate has a respective “Weight” calculated in relation to the Total Deposited Volume, calculated as follows:
Weight of the transaction:
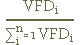
Where:
- Deposited Financial Value (VFDi): Financial value deposited in each extra-group Overnight DI rate transaction;
3. The series is divided into two (2) in a way that, in both directions, the sum of the defined weights does not surpass the defined Alpha value.
- Beta (β):
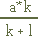 where:
where:
- l is the sum of the number of transactions in which l = [Li Number > 0] + 1
- k is the sum of the number of transactions in which k = [Ki Number > 0] + 1/li>
- K is the Max (0; a – Weight of the rate), calculated from the transaction with the lowest rate to the highest, with the count stopping when the calculation presents a zero value;
- K K is the Max (0; Kn-1 – Weight of the rate), calculated from the lowest rate to the highest, with the count stopping when the calculation presents a zero value;
- L is the Max (0; a – Weight of the rate), calculated from the transaction with the highest rate to the lowest, with the count stopping when the calculation presents a zero value;
- L is the Max (0; Ln+1 – Weight of the rate), calculated from the highest rate to the lowest, with the count stopping when the calculation presents a zero value.
When this L results in "0" (zero) the quantity of rates (l) is obtained.
When this K results in "0" (zero), the quantity of rates (k) is obtained.
- Gama (Y):
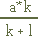 , where:
, where:
- l is the sum of the number of transactions in which l = [Number of Li > 0] + 1
- k is the sum of the number of transactions in which k = [Number of K1 > 0] + 1
- K is the Max (0; a – Weight of the rate), being calculated from the transaction with the lowest rate to the highest, with the count stopping when the calculation presents a zero value
- K is the Max (0; Kn-1 – Weight of the rate), being calculated from the lowest rate to the highest, with the count stopping when the calculation presents a zero value;
- L is the Max (0; a – Weight of the rate), being calculated from the transaction with the highest rate to the lowest, with the count stopping when the calculation presents a zero value
- L is the Max (0; Ln+1 – Weight of the rate), being calculated from the highest rate to the lowest, with the count stopping when the calculation presents a zero value;
When this L results in "0" (zero), the quantity of rates (l) is obtained.
When this K results in "0" (zero), the quantity of rates (k) is obtained..
4. The Beta (ß) and Gama (¿) calculation is carried out to adjust the weights of the upper and lower ends
For Beta calculation:
Q1 = Q1 shall be calculated only for the first transaction of the ascending order and its calculation will be the Max (0; Value of the Weight of the Transaction - Beta);
Q = Q shall be calculated as of the second transaction and its calculation will be the Max (0; Value of the Weight of the Transaction - Ri-1);
Ri-1 = Represents the R of the previous transaction (or R1 in the case of the previous transaction being the first);
R1 = R1 shall be calculated only for the first transaction of the ascending order and its calculation will be the Max (0; Beta – Value of the Weight of the Transaction);
R = The R shall be calculated as of the second transaction and its calculation will be the Max(0; Ri-1 – Value of the Weight of the Transaction)
For Gama calculation:
Qult = Qult shall be calculated only for the last rate of the ascending order and its calculation will be the Max (0; Weight of the Rate - Gama);
Q = Q shall be calculated as of the second rate and its calculation will be the Max (0; Weight of the Rate - Ri+1);
Ri+1 = Represents the R of the subsequent rate (or Rult in the case of the subsequent rate being the last one);
Rult = Rult shall be calculated only for the last rate in the ascending order and its calculation will be the Max (0; Gama – Weight of the Rate);
R = R shall be calculated as of the penultimate rate and its calculation will be the Max (0; Ri+1 – Weight of the Rate).
5. The final weights will be ascertained for calculating the Overnight DI Rate:
Calculation of the final weights:
The final weights shall be calculated for each transaction by using the following formula:
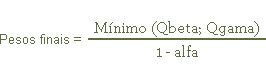
6. Final stage: Multiplication of the final weights by the DI Rates
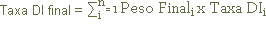
Where:
Final Weightii = Final weight ascertained for each rate;
DI Ratei = Overnight DI rate designated for extra-group transactions;
Final DI Rate = sum of the product of the Final Weight by the Overnight DI Rate in extra-group transactions on the date, rounded off to the second decimal place.
Precision Criteria:
| Code | Precision |
| VFD2 | two decimal places |
| Peso | nine decimal places WITH rounding off |
| Alpha | two whole numbers and four decimal places (% indicated on the monitoring screen) |
| Beta/Gama | nine decimal places WITH rounding off |
| k | whole; |
| l | whole; |
| K | nine decimal places WITH rounding off |
| L | nine decimal places WITH rounding off |
| Q | nine decimal places WITH rounding off |
| R | nine decimal places WITH rounding off |
| Final Weight | nine decimal places WITH rounding off |
| Dli Rate | Note: On the screen, the transaction can be informed with up to four decimal places, but for the calculation it is assumed that it will be rounded off to two decimal places |
| Final Weight X transaction Dii Rate | nine decimal places WITH rounding off |
| Final DI Rate | two decimal places WITH rounding off |
ESTATISTICS TO BE CALCULATED
The statistics listed below are calculated to provide further information on how the distribution is presented:
- Mode
- Median
- Minimum Rate
- Maximum Rate
- Variance
- Standard Deviation
- Coefficient of Skewness
- Kurtosis
DEFINITION AND EXPRESSION OF THE STATISTICS:
Mode (Mo)
Mode is the value that occurs with the greatest frequency in a distribution. As the variable being studied is the rate, the mode is defined as being the rate that occurs with the greatest frequency in the distribution named Modal Rate.
Median (Mnd)
The median is the average value or the arithmetic median between the central values in a distribution, i.e., the value that divides the distribution by 50% of the above observations and 50% below it. The median is the value of the Rate in this position within the distribution.
Minimum Rate and Maximum Rate
The Maximum Rate and Minimum Rate are considered to be the lowest and highest rate, respectively, observed within the distribution after the bilateral separation.
Standard Deviation (s) and Variance (s2)
To measure the dispersion of rates around the average, the Standard Deviation (s) and the Variance (s2) are used as expressed below:
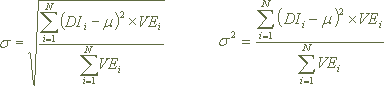
Where:
DIi is the DI rate of the i-th transaction, calculated to two (2) decimal places.
m is the average rate, calculated to two (2) decimal places.
VEi - is the Issue Value of the i-th transaction, informed to two (2 decimal places)
Coefficient of Skewness (a3)
The degree of a distribution deviation is named skewness. The second Pearson coefficient is used to measure the skewness of the distribution. The second Pearson Coefficient is defined by the following expression:
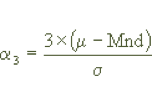
Where:
M is the ascertained average rate, calculated to two (2) decimal places.
Mnd is the ascertained median.
S is the calculated standard deviation.
Coefficient at the moment of Kurtosis (a4)
Kurtosis is the degree of flattening of a distribution in relation to a regular distribution.
In a regular distribution, the kurtosis coefficient is equal to three (a4= 3) and this is named a mesokurtic distribution.
A distribution with (a4 < 3) is named platykurtic, i.e., a flat-topped distribution, and a distribution with (a4 > 3) is named leptokurtic, a peaked distribution. The coefficient at the moment of kurtosis is defined by the following expression:
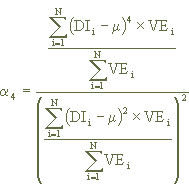
Onde:
DIi is the DI rate of the i-th transaction, calculated to two (2) decimal places.
M is the calculated average rate to two (2) decimal places.
VEi is the Issue Value of the i-th transaction, informed to two (2) decimal places.
The purpose of the statistics listed and calculated here is to parameterize each distribution and create a historical series of the parameters, thus enabling analysis of the distributions.
STATISTICAL CALCULATION CRITERION ON EXCEPTIONAL DATES
On exceptional dates in Brazil, for example, Carnival; Christmas; New Year; the national public holidays of January 20, January 25, April 23, July 09, November 20; and regional holidays in São Paulo and/or Rio de Janeiro, depending on the day of the week on which they fall, the market will operate the RI rate for one (1) and/or two (2) overnights. To resolve this situation the following criterion has been adopted for statistical calculation:
Using as an example Christmas in a year on which December 24 (business day) falls between Monday and Friday, the two stages of the special procedure adopted are described below.
Monday and Friday, the two stages of the special procedure adopted are described below. The totality of the transactions (population) refers to extra-group fixed rate DI issuances, registered on the B3 system.
1ª STAGE
Description of the calculation made on the business day immediately prior to December 24::
a)The population of DI issuances is selected with a one (1) business day term, whose rates are expressed in a year of 252 business days, in accordance with the following formula:
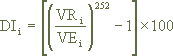
Where:
DIi is the DI Rate of the i-th transaction, calculated to two (2) decimal places.
VRi is the Redemption Value of the i-th transaction, informed to two (2) decimal places
VEi is the Issue Value of the i-th transaction, informed to two (2) decimal places.
b) É selecionada a população das emissões de DI, com prazo de 2 (dois) dias úteis, cujas taxas são convertidas para 1 overnight, expressas ao ano de 252 dias úteis, através da seguinte fórmula:
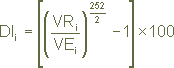
Where:
DIi, VRi e VEi are previously defined variables.
c) The two populations (one overnight and two overnights converted into one) are aggregated and the system proceeds to statistical calculation (average, mode, standard deviation, etc.) in accordance with the methodology published in Cetip Communications 113 and 114 dated January 26, 1998 and January 28, 1998, respectively.
2ª STAGE
Description of the calculation executed on December 24:
a) The population of DI issuances is selected with a one (1) business day term, whose rates are expressed and calculated as described in item "a" of the 1st stage;
b) The population of DI issuances is selected with a two (2) business day term registered on the business day immediately prior to the 24th, i.e., the same population of issuances considered in the 1st stage, whose rates are expressed and calculated as described in its item "b";
c) ) The two populations are aggregated and the system proceeds to statistical calculation in accordance with the Communications mentioned in item "c" of the first stage.
Methodology prepared by João Carlos Prandini, who holds a PhD in Mathematics from the University of São Paulo and is a Bloom Consulting director.